jueves, 7 de agosto de 2014
jueves, 17 de julio de 2014
FUNCIONES BIYECTIVAS
En matemáticas, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
En matemáticas, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
Formalmente, dada una función 
:
:
La función es biyectiva si se cumple la siguiente condición:
Es decir, si para todo 
de 
se cumple que existe un único 
de 
, tal que la función evaluada en es igual a .
de se cumple que existe un único de , tal que la función evaluada en es igual a .
Dados dos conjuntos e finitos, entonces existirá una biyección entre ambos si y sólo si e tienen el mismo número de elementos.
e finitos, entonces existirá una biyección entre ambos si y sólo si e tienen el mismo número de elementos.Teorema[editar]
es una 
existe y también es biyectiva.Ejemplo[editar]
La función:
es biyectiva.
Luego, su inversa:
también lo es.1
El siguiente diagrama de grafos bipartitos se puede ver cuando la función es biyectiva:
| Funciones | Inyectiva | No inyectiva | ||
| Sobreyectiva |
|  | ||
| No sobreyectiva |  |  |
Cardinalidad y biyectividad[editar]
Dados dos conjuntos 
y 
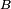, entre los cuales existe una función biyectiva 
tienen cardinales que cumplen:
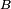y , entre los cuales existe una función biyectiva tienen cardinales que cumplen:
Suscribirse a:
Entradas (Atom)